Процедурные анимации - 1

(версия на английском)
Я решил разбить большой кусок информации под названием "процедурные анимации" на несколько маленьких. Не буду вдаваться в сложные загогулины, а постараюсь внести побольше практики. Итак, сегодня будем делать такое (с исходником и множеством гифок!):

Зачем? Во-первых, мне это пригодится позже (в выпуске, эдак, четвертом)... во-вторых, для получения подобного движения нужно понимать много всякого в математике. Получается, это вроде и учебная анимация, но вроде как и веселая на вид.

Движение по окружности

Сначала разберемся, что такое окружность и как по ней заставить двигаться точку. Вспоминая математику, посмотрим на картинку и запишем выражения для x и y:

x = r*cos(a)

y = r*sin(a)

Теперь, увеличивая все время угол a, можно добиться движения по окружности:

Это хорошо, двигаемся дальше...

Меняющийся радиус

Давайте смотреть на изначальную гифку:

Это уже не просто движение по окружности. Рисуются какие-то лепестки. Если посмотреть на наши формулы для x и y, то заметим нетронутый радиус окружности r. Угол a мы меняем для самого движения. А с радиусом что? Как мы знаем радиус - это всего лишь число, указывающее на расстояние от центра окружности до его точек. А что, если его менять во время движения?

Спираль

Например, пусть радиус меняется так же, как и угол:

r = a * 0.1

Тогда траектория движения будет такая:

Спиралька... Супер! Но нам ведь надо, чтобы радиус менялся "туда-сюда", а не просто увеличивался до бесконечности. В этом нам снова помогут косинусы-синусы, которые как раз периодические и "то увеличиваются, то уменьшаются", постоянно крутясь вокруг нуля.

Лепестки

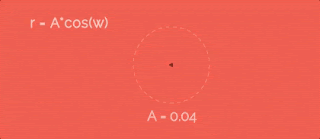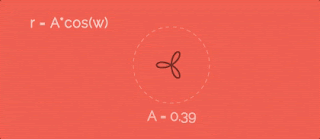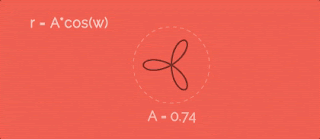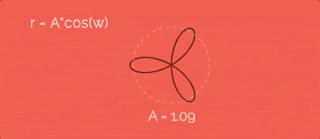
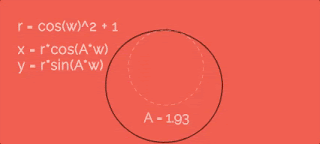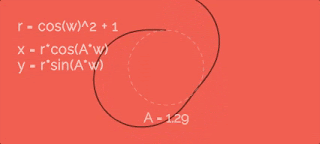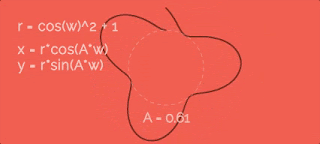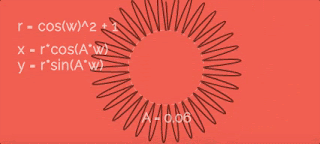
Увеличиваем радиус по косинусу с некоторой скоростью w. Чтобы было понятно, я заснял гифку, на которой видно какая была бы траектория при разном значении параметра A. Итак, видно, что чем больше коэффициент A - тем больше лепестки.

Давайте добавим единицу в r, чтобы точки отошли от центра окружности... вот так:

Уже лучше, но я не хочу, чтобы значение r было меньше 1, а ведь косинус "то больше 0, то меньше" - и из-за этого общее значение радиуса становится меньше 1, а при больших A даже меньше 0!

Квадрат (^2)

В знакопеременных случая ("то меньше 0, то больше") помогает квадрат! Не фигура, а функция возведения в степень. Вроде того, что x*x - всегда больше либо равно нулю.
Смотрим:

Класс! То, что нужно!
Можно брать код и использовать у себя... но давайте подождем еще чуть-чуть, ведь мне надо признаться, что я немного схитрил...

Скорость изменения радиуса

В формулах я использую w как некую "скорость изменения радиуса". Это правда так - но чему оно равно? На всех приведенных выше гифках эта скорость втрое больше, чем скорость движения точки по окружности (переменная a из первых формул для x и y). Звучит как-то странно, что именно втрое, да? Чтобы развеять все сомнения, сейчас сделаем вот какую штуку.
Давайте посмотрим, как вообще этот параметр сказывается на фигуре-пути:

Получается, если хотим два лепестка - скорости должны быть одинаковые, если четыре - в два раза отличаться. А у нас шесть лепестков - значит точка по окружности должна двигаться в три раза медленнее, чем меняется радиус.
Вот и вся магия!

Итоговый код

Осталось положить ссылку на исходный код и наслаждаться вот таким движением:

Стоп! "Но на изначальной гифке движение прикольно тормозится во впадинах!" - воскликнет любой... Да, и это тоже сделано отдельной математической формулой. Но давайте отложим это на следующий тутор... Договорились?

Сообщения, схожие по тематике: