Hi! I'd like to split the big tutor about "procedural animations" to small parts. So, this is the first one. I will concentrate on practice and animation. So, today we will make this one (with source code and gifs!):
Why this? On the one hand I will use it later (in part 4, I guess)... on the other hand to make this animation we should understand a lot of math stuff. So, this example will be like an introduction for us. Let's start making this fun procedural animation!
Circular motion
First of all let's remember what is a circle and how we can animate point's movement by a circle. Math says that we should use cosine and sine functions. Let's take a look on this picture and write down expressions for x и y:
x = r*cos(a)
y = r*sin(a)
Ok, by increasing angle a we can set up the circular movement:
Great! Let's go further...
Changable radius
This is the result the I want to achieve:And this is not a simple circular movement. This is more like a flower with six petals. Let's return to our formulas for x и y. And let's think about circle's radius r. Yes, we are increasing the angle a all the time, but what about the radius? It's just a value that shows the disctance between circle's center and circle's points. What if we change it while moving?
Spiral
For example, let's animate the radius in the same way as an angle:r = a * 0.1
And the path for this movement is:
Flowers and petals
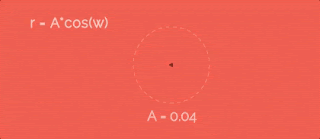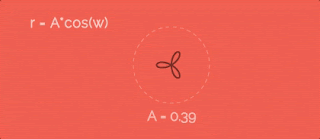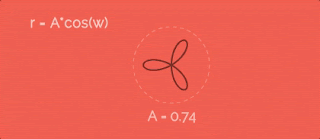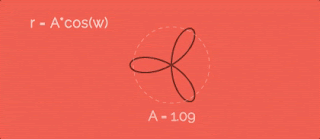
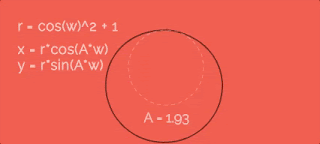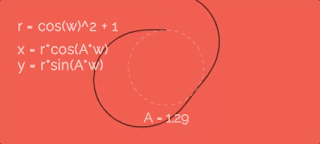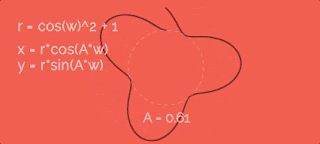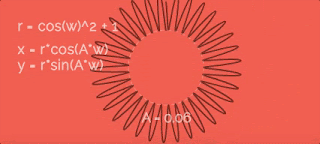
Let's increase radius by cosine function with some velocity w. To make it more obvious I recorded gif so we can look at point's paths with different A. So, as greater A as more petals.Let's add 1 to the r equation. In this case the path will be further from the cener... like this:
Better! But values of r are less than 1 a lot of time. This is because cosine has positive and negative values. And I want just positive. What should I do?
Square (^2)
The square helps in cases with alternating functions (with positive and negative result values). I mean not a figure 'square' but the function x*x. This function is great because the result is always positive.Yay! This is what we need!
Ok, now we can grab the code and use it... but hold on just a second, I'd like to confess that I've made one trick...
Changing radius speed
Ok, in equations I used w like "speed of the radius changes". Yes, it is true - but what is the value of this speed? In all previous gifs this speed is in three times greater than the speed of circular movement (the variable a from equations for x and y). Sounds great, but why exactly "three times"? To be sure look at the gif. Here you can find how this value changes the entire path:So, if we want just two petals - speeds should be equal, if four - two times greater. And we have six petals in our path - so the speed is in three times greater.
The magic is over :)
Source code
Ok, here is the source code of the animation. Just look and relax:Stop! "But there are slow-mo things after each petal on the original gif!" - everyone says... Yeah, you are right. And there is additional math formulae for this.
But let's code this in next tutorial... ok?







0 коммент.:
Отправить комментарий