Параллакс: звездное небо в 2д и не только

Всем привет! Наверно, немногие помнят, что когда-то давно я начинал делать стратегию на космическую тематику. Тогда я продвинулся недалеко, причин тому было много, но они все по большей части бытовые отговорки. Но не будем об этом, скажу, что единственно полезное, что я тогда сделал - навигацию по 2д звездному небу. Хитрость довольно простая, но я решил описать ее здесь, чтобы журнал не пустовал, а, наоборот, набирал полезностей на своих страницах. Итак, начнем!

Задача - отобразить что-то вроде звезд на небе и сделать адекватную навигацию (скроллинг) по ней. Для этого разобьем задачу на две подзадачи:

• отображать элементы неба на плоскости, учитывая их "глубину" в небосводе
• плавно сдвигать камеру "слежения" за небом

Казалось бы, GlScene - трехмерный движок, почему бы не воспользоваться его возможностями? Ответ прост - мне нравится 2д, зачем же тогда стрелять из "пушки по воробьям"? Тем более, что возможности 3д-движка не всегда под рукой и нужно уметь делать простые вещи самому.

Итак, по сути нам придется "вручную" проецировать звезды из 3d-пространства на плоскость экрана. Как же это делается?
Все предельно просто. У нас есть камера-глаз, с помощью которого мы проецируем трехмерное изображение расположения звезд на плоскость-экран. Схематично, это можно представить с помощью картинки:

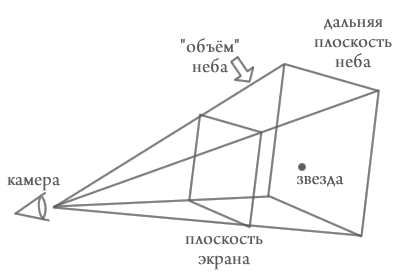
Для простоты проведения расчетов посмотрим на эту картинку сверху, чтобы увидеть искомое на двумерном рисунке:

Теперь все становится очевидным, из подобия треугольников находим положение звезды на экране, зная ее положение на небосводе:

X = ПолуширинаЭкрана * (1 + (Расстояние до камеры) * (Координата X звезды) / (Координата Z звезды))
Аналогично для Y-координаты:

Y = ПолуширинаЭкрана * (1 + (Расстояние до камеры) * (Координата Y звезды) / (Координата Z звезды))

где
X - координата звезды после проекции на экран (значение в пикселях, левый верхний угол экрана имеет координаты (0, 0)),
ПолуширинаЭкрана - размер половины экрана в пикселях
Расстояние до камеры - расстояние от камеры до плоскости экрана
Координата X звезды - коордианата X звезды в мировых координатах (в 3д пространстве)
Координата Z звезды - коордианата Z звезды в мировых координатах (в 3д пространстве, отсчет ведется от камеры).
В скобках появляется "1 + " из-за того, что мы примем, что звезда, находящаяся по оси OX в 0-ой координате, проецируется в центр экрана. Подставив "Координата X звезды" равной нулю, можно убедиться в этом.

На языке программирования наши математические формулы примут следующий вид:

StarPos := VectorSubtract(Items[i], fCamera.Position.AsVector);
StarPos[0] := fScreenSizes[0]/2 * (1 + fCameraDistance * StarPos[0] / Items[i][2]);
StarPos[1] := fScreenSizes[1]/2 * (1 + fCameraDistance * StarPos[1] / Items[i][2]);

Чтобы немного изменять размеры звезд (ближние сделаем побольше, а дальние сделаем поменьше), применим небольшой прием, изменяя значение StarSize, который впоследствии используется при задании высоты и ширины спрайта:

StarSize := 10 * 1 / Items[i][2];

То есть сделаем его обратнопропорциональным Z-координате звезды. Коэффициент 10 - это изначальный размер текстуры изображения с кружком.
Хм... итоговый код рендера звезд запишется в простом виде:

Procedure TfrmDemo1.OnDirectRender(Sender: TObject; var aRenderInfo: TRenderContextInfo);
var
  i: integer;
  StarPos: TVector;
  StarSize: Single;
begin
  for i := 0 to fStarsPositions.Count - 1 do
    with fStarsPositions do
    begin
      StarPos := VectorSubtract(Items[i], fCamera.Position.AsVector);
      StarPos[0] := fScreenSizes[0]/2 * (1 + fCameraDistance * StarPos[0] / Items[i][2]);
      StarPos[1] := fScreenSizes[1]/2 * (1 + fCameraDistance * StarPos[1] / Items[i][2]);
      StarPos[2] := 0;

      StarSize := 10 * 1 / Items[i][2];
      fglStar.Position.SetPoint(StarPos);
      fglStar.Width := StarSize;
      fglStar.Height := StarSize;
      fglStar.Render(aRenderInfo);
    end;
end;

По сути, в этом коде идет простой перебор по всем звездам, для каждой из которых выполняются вышеописанные математические действия.

Осталось теперь только заняться камерой. Опишем ее такой структурой:

fCamDestPosition: TVector;
fCamSpeed: TVector;

Первый вектор для хранения желаемого положения камеры (куда она стремится как бы). Второй вектор - для задания скорости движения камеры из текущего положения в желаемое. При движениях мыши будем менять желаемое положение камеры (но не положение самой камеры!). При "тиках" cadencer'а - будем двигать саму камеру.
Исходя из вышесказанного, код движения напрашивается сам собой в OnProgress, но я еще для красоты вынес движение камеры в отдельную процедуру:

Procedure TfrmDemo1.UpdateCamera;
var
  Dir: TVector;
begin
  with fCamera.Position do
  begin
    Dir := VectorSubtract(fCamDestPosition, AsVector);
    fCamera.Position.SetPoint(VectorAdd(AsVector, VectorScale(Dir, fCamSpeed)));
  end;
end;

А вот изменение желаемого положения камеры осталось в TfrmDemo1.OnCadencerProgress:

if IsKeyDown(VK_LButton) then
  fCamDestPosition := VectorAdd(fCamDestPosition, VectorScale(fMouseDelta, 1/100));

Вот и все. Теперь мы со спокойной совестью можем запустить программу и увидеть кружки-звездочки, плавно сдвигающиеся при передвижениях камеры. Чтобы не быть голословным я даже записал видео происходящего:

Исходные коды на Delphi можно забрать отсюда.
По сути мы реализовали обычный параллакс, с чем всех нас и поздравляю!

Я вообще надеялся порадовать бесконечным небом, но как-то не сложилось. Нужно каким-то образом перебрасывать звезды в видимую область экрана, чтобы поддерживать небо звездным, куда бы мы ни сместили камеру. Возможно, обновлю демку чуть позже, сейчас же простого решения не напрашивается в голову.
В чем бонус того, что мы выполнили все вычисления сами, не прибегая к возможностям 3d-движка? Ну, теперь эти формулы можно с легкостью перенести, например, на flash, hge, popcap и все будет работать и радовать глаз...
Кстати, в стратегии на космическую тему, что я начинал делать, звездный фон выглядел практически в неизмененном виде, только звезды отображаются крестиками и их плотность на небе невелика (но мне нравилось, в принципе):

Можно еще сильнее доработать демку и вместо random-ного выставления координат звезд (в процедуре InitStars), использовать какую-нибудь заготовленную схему... в принципе, если сильно постараться, можно получить что-то подобное:

Также нужно понимать, что эта техника дает превосходный результат в скроллинг-играх при столь малых затратах на расчеты. При виде сбоку или сверху смещается игрок - за ним смещаем камеру, а задние фоны отрисовываем параллакс-методом. То есть совсем дальние с меньшей скоростью, ближние - с большей.
Вот наглядный пример (сдвигаем камеру влево-вправо при движениях мыши с зажатой клавишей):

Создан на flash, и при этом я пользовался точно теми же формулами, что мы выводили выше для Delphi. Арт не мой, я "позаимствовал" его из замечательной игры Coma.

p.s. Вот такими простыми сообщениями-уроками я наводняю журнал. Надеюсь никому не скучно?!

Сообщения, схожие по тематике: